Problema 9.

Determina las dimensiones de una piscina abierta al aire, de volumen 32 m³, con un fondo cuadrado y con la misma profundidad en todos sus puntos, de manera que la superficie de sus paredes y del fondo sea mínima.

Solución:

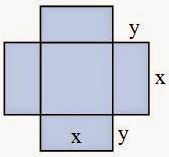
Si llamamos x al lado del cuadrado que forma el fondo de la piscina e y a la profundidad, en el dibujo siguiente se muestra la superficie de sus paredes y del fondo:

Por tanto, se deduce que la función superficie que queremos minimizar es:

S (x, y) = x² + 4 x y

Como el volumen de la piscina es 32 = x² y, despejamos la variable y de esta ecuación:

y = 32 / x²

La sustituimos en la función S para que esta función dependa sólo de la variable x:

Derivamos la función e igualamos a cero para buscar el mínimo relativo:

Comprobamos que se trata de un mínimo:

Si x = 4, se verifica que y = 32/16 = 2 m.

Así, la piscina debe medir 2 m de profundidad y su base 4 m de lado.