Un ganadero tiene su casa, de planta
rectangular, situada en el centro de una pradera y rodeada toda ella de hierba.
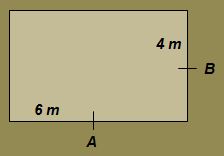
Las dimensiones de la planta de la casa son 12 y 8 metros.
El granjero clava dos cadenas en las paredes
exteriores de la casa en las que poder atar a su caballo y las sitúa en los
puntos A y B que aparecen en el siguiente dibujo (son los puntos medios de los
lados), donde el rectángulo representa la planta de la casa.
La cadena situada en A tiene 4 metros de
longitud y la situada en B tiene 5 metros.
Si un día sujeta a su caballo con la cadena
del punto A y al día siguiente lo hace con la cadena del punto B, ¿qué
superficie de hierba podrá comer el caballo entre los dos días?
Solución:
El
dibujo correspondiente a la superficie que puede comer el caballo entre los dos
días es el siguiente:
Esa superficie de hierba que puede comer es la coloreada de
verde en el dibujo. Y está compuesta por:
- Un
semicírculo centrado en A y cuyo radio es de 4 m.
- Un
semicírculo centrado en B y cuyo radio es de 5 m.
- Dos
cuartos de los círculos centrados en los vértices del lado de 8 metros, y cuyos
radios miden 1 m (que equivalen a un
semicírculo de radio 1 m).
Por
tanto, dicha superficie es:
Si
sustituimos el valor de 𝜋
por la aproximación 3,14, resulta que la superficie de hierba que podrá comer
el caballo entre los dos días es de, aproximadamente, 65,94
m 2.




No hay comentarios:
Publicar un comentario